Finding the Most One-Dimensional Popular Artist
If you’re like me, when you listen to music, you sometimes catch yourself thinking, “This band is so one-dimensional. All of their songs sound the same!”
When I had this experience again recently, I finally decided to find out whether anyone had ever written about this. I found tons of websites and discussions listing bands that authors think are one-dimensional, but it seemed like nobody had actually tried to quantify it.
This post is my stab at doing just that. Using math and data gathered from the Spotify API, I’m going to try to answer the question of which popular artists are the most one-dimensional. I’m only going to use an artist’s top 10 tracks to represent their “sound”. So really, I’m measuring which artist’s top hits are the most one-dimensional.
Ideally, I’d use their entire discography. But the time required to effectively filter and clean that data from Spotify’s API is massive, so this will have to do.
Before I get started with the Spotify data, though, I need to define one-dimensionality in some kind of mathematical way.
If you don’t care about the math or the data and just want to see the results, skip to the Ranking the Spotify Global Top Artists of 2012-2016 section at the bottom.
Defining One-Dimensionality Mathematically
When I say an artist is one-dimensional, I’m really saying that the characteristics of their songs are all really similar. There’s very little variety in their sound. The goal, then, is to represent this concept mathematically so I can actually quantify how similar an artist’s songs are.
To do that, I’ll try to capture how close together these songs are in some K-dimensional vector space defined by the number of song characteristics I think impact how I perceive the sound (or in this case, the number of relevant characteristics Spotify gives me access to).
Within that mathematical framework, I can represent each song as a vector and calculate how tightly packed together an artist’s songs are.
Sounds good in the abstract, but I need to get more specific.
Cluster Spread
I’ll define an artist’s cluster spread as the sum of the squared distances of a given song vector to the center of all the song vectors, summed over every song. Any definition of distance will have its own issues, but this seems like a pretty good way to measure how spread out a cluster is since:
- If all song features range from 0 to 1, the squared distance reduces the impact of any individual song.
- I’m using the top 10 tracks for every artist, making a summation-based metric comparable across artists.
Mathematically,
\[CS = \sum_{s=1}^{10}\sum_{i=1}^{k}(x_{i} - c)^{2}\]This can be a little confusing. It’s easier to get the intuition of this metric visually, by looking at two made-up examples.
Visualizing One-Dimensionality
In the pictures below, the red X represents the center of each cluster of three points. The red, blue, and green lines connect each point to the center. I’ve connected the points into a triangle to help illustrate how one group of points is more tightly knit than the other.
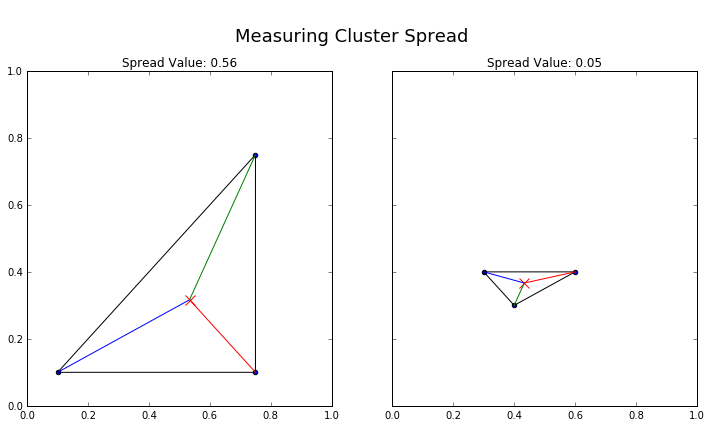
It’s clear that the triangle on the right is more compact than the triangle on the left. The red, blue, and green lines are much smaller.
The Cluster Spread metric captures that difference. The value for the right triangle is much smaller than the value for the left triangle, which means it’s more compact.
It’s easy to see how this works in two dimensions. While I can’t visualize how this works in eight dimensions, the logic extends perfectly. I can use my Cluster Spread metric to measure the spread of any set of points in 8-D space just like I did in the 2-D space above.
With the math taken care of, it’s time to move on to the music.
Spotify Audio Features Data
The Spotify API is awesome. Most importantly, for this project, Spotify provides access to audio features for any song in their collection. Audio features are characteristics of songs like danceability, energy, and loudness that Spotify has assigned numerical values to represent.
I decided to use eight of the features. I picked ones that naturally lend themselves to being ranked numerically (so I didn’t use things like the key and time signature, but did include things like how acoustic the song is). The eight characteristics I chose are:
- Acousticness
- Danceability
- Energy
- Valence (a measure of the song’s positiveness (happiness, cheerfulness, etc.))
- Instrumentalness
- Loudness
- Speechiness
- Tempo
With these features, I can represent each song as an 8-dimensional vector. I did a little bit of data transformation to scale all the features to between 0 and 1, since I don’t want any one feature to dominate the spread metric.
And that’s all there is to it. With my Cluster Spread formula, my features chosen, and the data from Spotify’s API, I’m ready to start ranking artists.
Ranking the Spotify Global Top Artists of 2012-2016
At the end of every year from 2012 to 2016, Spotify released a playlist of their Global Top 100 Tracks of the Year. There are several hundred artists featured on these playlists, and I ranked all of the artists above a baseline popularity threshold.
In total, I ranked about 200 artists. The 10 most one-dimensional artists with top hits from 2012-2016 are:
| Rank | Artist | Cluster Spread Value |
|---|---|---|
| 1 | Kesha | 1.72 |
| 2 | Foster The People | 1.86 |
| 3 | Fall Out Boy | 1.93 |
| 4 | American Authors | 1.94 |
| 5 | PSY | 1.95 |
| 6 | DNCE | 1.98 |
| 7 | Carly Rae Jepsen | 1.99 |
| 8 | Alesso | 2.03 |
| 9 | WALK THE MOON | 2.03 |
| 10 | Robin Schulz | 2.07 |
These look pretty good to me! Artists like Kesha, PSY, and Carly Rae Jepsen are classic examples of one-dimensional bands you might have picked before reading this.
While I won’t say this is the definitive ranking, and I chose the audio features I personally thought were relevant, I think this is the best anyone has done so far.
Kesha Wins Most One-Dimensional of All Time
After ranking artists from the 2012-2016 Top 100 Tracks playlists, I wanted to evaluate some classic artists across time periods.
I didn’t calculate Cluster Spread for every major group in history, but I did try a lot of bands (at least another 75-100). In a nail biter, Kesha managed to beat out Creed (a heavy favorite going into this process) as the most one-dimensional of all time.
But don’t worry Creed fans. There’s always a chance they’ll come out of retirement and write a new hit that will take them higher.
For those interested in recreating or expanding this analysis, the Jupyter Notebook with all the code can be found in the Github repository for this post.


Leave a Comment